index.md

layout: default
title: Camera basics
nav_order: 2
mathjax: true

Camera basics

{: .no_toc}

Table of contents

{: .no_toc .text-delta }

1. TOC {:toc}

What is a camera?

A modern definition of a camera is any device capable of collecting light rays coming from a scene, and recording an image of it. The sensor used for the recording can be either digital (e.g. CMOS, CCD), or analog (film).

The pinhole camera

The term camera is derived from the Latin term camera obscura, literally translating to "dark room". Earliest examples of cameras were just that; a hole in a room/box, projecting an image onto a flat surface.

Using only a small hole (pinhole) blocks off most of the light, but also constraints the geometry of rays, leading to a 1-to-1 relationship between a point on the sensor (or wall!) and a direction. Given a 3D point

(x,y,z)

in space, the point on the sensor

(u, v)

is given by:

\begin{cases} u = f \frac{x}{z}\\ v = f \frac{y}{z} \end{cases}

in which

f

is the focal length: the distance from the pinhole to the sensor. Multiple 3D coordinates fall onto the same sensor point; cameras turn the 3D world into a flat, 2D image.

Let's make the sensor coordinate system more general, by introducing an origin

(u_0,v_0)

and non-isotropy in the

x

and

y

focal lengths, which is necessary to describe non-rectilinear sensors. The complete pinhole camera model can be summarized by a single affine matrix multiplication:

$$ \begin{bmatrix} uw\ vw\ w \end{bmatrix}

\begin{bmatrix} f_x & 0 & u_0\ 0 & f_y & u_0\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x\ y\ z \end{bmatrix} := K \begin{bmatrix} x\ y\ z \end{bmatrix} $$

The matrix

K

is known as the intrinsic parameters matrix. Let's complete our model by adding an arbitrary rotation/translation to the world coordinate system. A single matrix multiplication can relate world coordinates

(x_w,y_w,z_w)

to camera-centric coordinates

(x,y,z)

:

$$ \begin{bmatrix} x\ y\ z \end{bmatrix}

\begin{bmatrix} R_{11} & R_{12} & R_{13} & t_x\ R_{21} & R_{22} & R_{23} & t_y\ R_{31} & R_{32} & R_{33} & t_z\ \end{bmatrix} \begin{bmatrix} x_w\ y_w\ z_w\ 1 \end{bmatrix} := \begin{bmatrix} R | t \end{bmatrix} \begin{bmatrix} x_w\ y_w\ z_w\ 1 \end{bmatrix} $$

where

R

is an orthogonal rotation matrix, and

t

a translation vector. The

\begin{bmatrix}R\|t \end{bmatrix}

matrix is known as the extrinsic parameters matrix. We can combine intrinsic and extrinsic parameters in a single equation:

$$ \begin{bmatrix} uw\ vw\ w \end{bmatrix}

K \begin{bmatrix} R|t \end{bmatrix} \begin{bmatrix} x\ y\ z\ 1 \end{bmatrix} $$

When using more than one camera, it is useful to have a single world coordinate system while letting each camera have its own sensor coordinate. As explained in the next section, if intrinsic and extrinsic parameters are known for every camera looking at the scene, 3D reconstruction can be achieved through triangulation.

Sensor

Coordinates

Continuous sensor coordinates make sense when simply projecting an image or recording it with a film. If using a digital sensor, a natural choice for the sensor coordinate system is the pixel indices. Those discrete, unitless values can be related to the physical sensor by defining an equivalent focal length in pixel units:

The image plane is an imaginary construct sitting in front of the sensor, at one focal length (in pixels) away from the camera's coordinate system. Because it sits in front of the camera, the image is upright again.

It is common to choose the

z

axis to point toward the scene, and the

y

axis to point downward. This matches the conventional downward-pointing vertical coordinates in pixel coordinates, with

(u,v)=(0,0)

in the top-left corner.

Technologies

We'll focus on the two main families of digital sensors: CCD and CMOS.

In both families, the actual light sensing is based on the electron-hole pair generation in MOS devices.

CCD

In CCD sensors, the generated charges in the photodiodes are accumulated under a potential well, controlled by a voltage on the gate.

Charges can be moved to a neighboring pixel by performing a specific sequence on the gates. By shifting the charges all the way to the edge of the sensor, individual pixel values can be readout sequentially.

Advantage of CCD sensors include the simplicity of their design, and the large surface dedicated to sensing light. One disadvantage is the readout speed bottleneck caused by using a single decoding unit.

CMOS

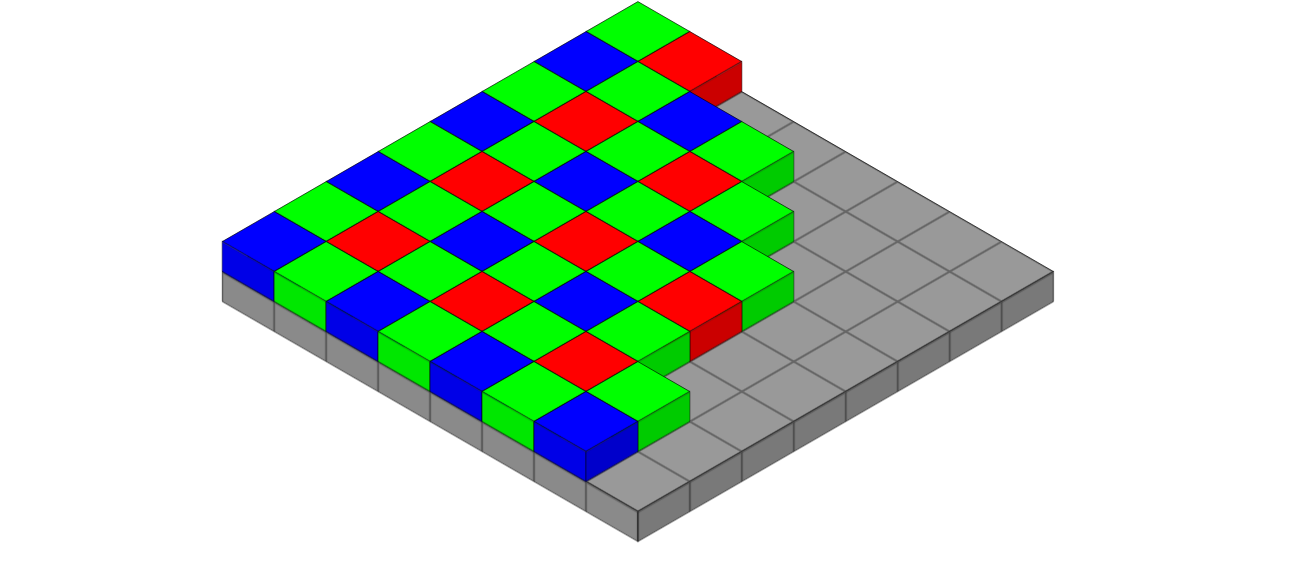
Bayer filter

Lens

Distortion

Aperture

Shutter

Mechanical shutter

Electronic shutter

Photography basics

The 3 parameters

• Aperture
• Shutter speed
• ISO

Each parameter can be converted to a

\log_2

scale. A common name for a unit on that scale is a stop. For example, increasing exposure by one stop can be achieved by doubling the shutter speed, doubling the ISO or increasing the aperture by

\sqrt{2}

.